
先生!\(3^(10)\)の桁数を求めよという問題がわかりません!

それは、常用対数を利用するんだよ。問題の中に、3の常用対数の値が書いてないかい?

あっ書いてます!でもどうやって使えばいいのか、、、

じゃあ一緒に見ていこう!
目次
常用対数の桁数と最高位の数とは?
はじめは概念的な話になるので、飛ばしてもらっても大丈夫です!
そもそも桁数と最高位の数とは?
桁数は、皆さんご存じの通り、100は3桁、1000は4桁という具合ですね。では、最高位の数字とは何でしょうか。最高位とは、一番大きい桁の事を指します。例えば、1200であれば1、45000であれば、4となります。ここまでは皆さん当然お分かりかと思います。
常用対数って?
では、次に常用対数について学習しましょう。常用対数は簡単に言えば、その数が10の何乗かです。例えば、1000であれば10の3乗なので、\(\log_{10}1000=3\)となります。
常用対数は、桁数のほかにも色んな分野に応用できるので、各値の近似値が決められています!
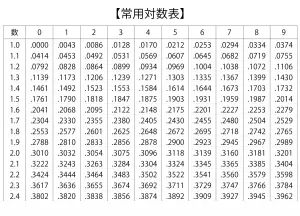
例えば、1.22の常用対数は、0.0864となります!
桁数についての考え方:常用対数
対数の基本定理
常用対数についての話の前に、後に用いる対数の基本定理を紹介します。
基本定理
\(z=xy\)とする。そのとき、
$$\log_{10}z=\log_{10}x+\log_{10}y$$
$$\log_{10}t^n=n\log_{10}t$$

なんだか、抽象的でわかりずらいなあ

例えば\(\log_{10}6=\log_{10}3+\log_{10}2\)、
\(\log_{10}2^(10)=10\log_{10}2\)といった感じのことだよ

あっそれならわかります!

もう1問応用問題を見ていこう!!
桁数の考え方
突然ですが、はじめに自然数mの桁数について考えてみましょう。
mの桁数がnの場合、次の式が成り立ちます。$${10^(n-1)}\leq{m}\lt{10^n}$$イメージ感としては、3桁の数字aは、\({10^2}\leq{a}\lt{10^3}\)が成り立つという感じです。
次に、先ほどの不等式で常用対数を取ります。底10は1より大きいので不等式はそのまま成り立ちます。$${n-1}\leq{\log_{10}m}\lt{n}$$
この考えは逆に考えることもできます!つまり、\({n-1}\leq{\log_{10}m}\lt{n}\)が成り立てば、nはmの桁数に相当します!実際に、\({n-1}\leq{\log_{10}m}\lt{n}\)が成り立てば、\({10^(n-1)}\leq{m}\lt{10^n}\)。よって、nはmの桁数となります!
桁数の問題:実践編
恐らくまだ抽象的なので、実践例題で見ていきましょう!
例題
\(3^(10)\)の桁数を求めよ。ただし、\(\log_{10}3=0.4771\)
解答
\(3^(10)\)の常用対数をとると、$$\log_{10}3^(10)=10\log_{10}3={10}\times{0.4771}=4.771$$
ゆえに、\({4}\lt{\log_{10}3^(10)}\lt{5}\)
よって、\({10^4}\lt{3^(10)}\lt{10^5}\)
故に、\(3^(10)\)の桁数は、5

次は、最高位の数について考えよう!
最高位の数を求める:常用対数の利用
最高位の数:考え方
先ほどの続きとして、\(3^(10)\)の最高位の数を考えていきましょう!桁数は5なので、最高位の数をmとおいてみましょう。すると、次の式が成り立ちます。$${{m}\times{10^4}}\leq{3^(10)}\lt{{m+1}\times{10^4}}$$
この式で常用対数を取ると、$${4+\log_{10}m}\leq{10\log_{10}3}\lt{4+\log_{10}(m+1)}$$
先ほど同様、この誘導は逆に考えることもできます!

なんだか桁数に比べて分かりずらいなあ

具体的な値で見てみると、分かりやすいよ!
最高位の数:実践問題
実践例題
\(3^(10)\)の最高位の数を求めよ。ただし、\(\log_{10}2=0.3010\),\(\log_{10}3=0.4771\)
解答
\(3^(10)\)の常用対数をとると、$$\log_{10}3^(10)=10\log_{10}3={10}\times{0.4771}=4.771$$
ここで、与えられた値から次がわかる$$\log_{10}5=\log_{10}(\frac{10}{2})=1-\log_{10}2=1-0.301=0.699$$
$$\log_{10}6=\log_{10}({3}\times{2})=\log_{10}3+\log_{10}2=0.301+0.4771=0.7781$$
したがって、$${4+\log_{10}5}\lt{\log_{10}3^(10)}\lt{4+\log_{10}6}$$
よって、$${{5}\times{10^4}}\lt{3^(10)}\lt{{6}\times{10^4}}$$
したがって、求める最高位の数は5
まとめ
今回の記事はいかがでしたか?
ポイント
・桁数を取るときは、常用対数を取れば、解決!
・最高位の数を求める時は、自分で不等式を作成!










