試験で頻出の金属結晶ですが、皆さんどのような印象をお持ちですか。
理解が曖昧で完答できない人や、計算が大変だからと毎回避けてしまっている人はきっと多くいるでしょう。
実はそれ、非常に勿体無いです。
金属結晶では、出題される内容は決まっています。したがって、いったん完璧に理解してしまえば、確実に得点できる分野なのです。
そこで今回は、ただ知識をお伝えするだけでなく、なぜそうなるのかについても丁寧に解説していきたいと思います。
何度も読み込めば、もう金属結晶でつまずくことはなくなるでしょう。
プロフィール

目次
金属結晶の結晶格子
まずは金属結晶の結晶格子の位置づけを確認しておきましょう。
今回扱う範囲は次の図における赤い囲みの部分になります。結晶の中の1種である金属結晶について、どのような結晶格子があるのかを見ていくことになります。
図中にも書かれていますが、金属結晶がとる代表的な結晶格子は3つあります。面心立方格子・体心立方格子・六方最密構造の3つです。
ここからそれぞれについて具体的に見ていくのですが、金属結晶の結晶格子を学習する際に覚えるべきことは決まっています。
含有粒子数・配位数・格子の辺と原子の半径の関係・充填率の4つです。したがって、各結晶格子がこれらの項目についてどのような特徴があるのかをしっかりと覚えるようにしましょう。
なお、結晶格子の全体像およびこれらの用語の意味については下の記事を参考にしてください。
体心立方格子
体心立方格子は立方体の頂点と中心に原子が配置されています。
含有粒子数ですが、中心に1つ存在し、8つの角に1/8の粒子が含まれていることから次のようになります。
また、配位数は中心の原子に注目してみれば8であることがわかります。
続いて 単位格子1辺と原子の半径の関係を、単位格子1辺をa、原子の半径をrとして求めます。aとrの関係を求める際は、基本的には球同士が接している面を切り出して考えるのがセオリーです。
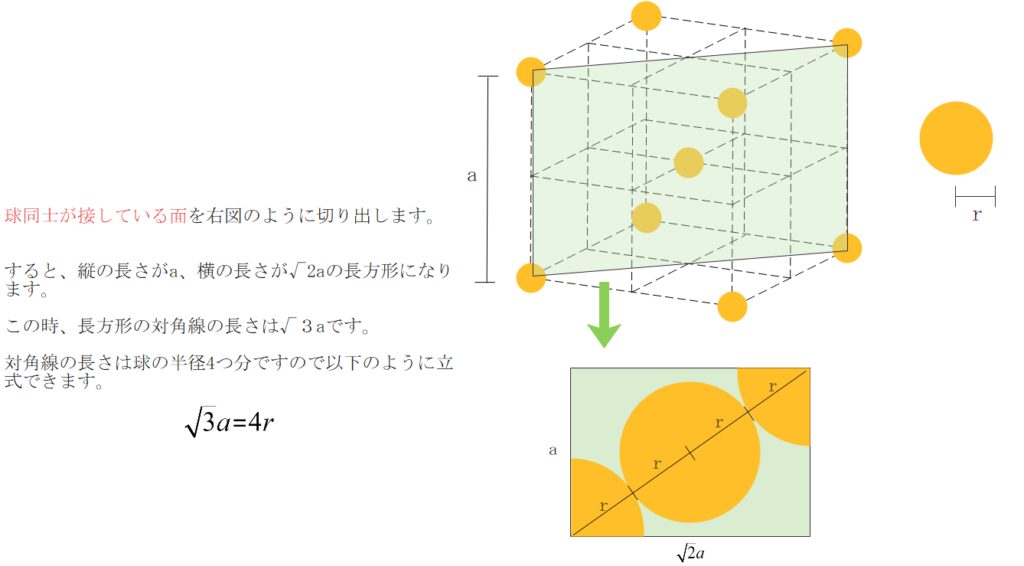
次に、充填率を求めます。充填率は次の式で求めることができます。
充填率=粒子が占める体積÷格子の体積
体心立方格子の場合、粒子は2つあるので次のようになります。
したがって、体心立方格子の充填率は68%となります。
面心立方格子
面心立方格子は立方体の頂点の他、各面の中心に原子が配置されています。
含有粒子数は、各頂点に1/8の粒子が、各面の中心に1/2の粒子がいることから、次のようになります。
次に、配位数について考えてみましょう。いくつになるでしょうか。
実は面心立方格子の配位数というのは体心立方格子のように簡単には出すことができません。立方体の中心に原子がいないからです。
そのため、面心立方格子の配位数は結晶格子を2つくっつけることで数えやすくします。
このように2つの立方体を並べて赤い粒子に注目すると、周りのピンク色の粒子が最近接していてその数は12であることがわかります。したがって、面心立方格子の配位数は12となります。
では次に、aとrの関係を求めてみましょう。
最後に充填率を求めます。面心立方格子の場合、含有粒子数は4であるので、次のような式になります。
したがって、充填率は74%になります。
六方最密構造
それでは金属結晶の結晶格子の3つ目である六方最密構造についてみていきましょう。
今までの体心立方格子と面心立方格子と比較すると出題頻度は低いですが、難関大レベルになると問われてもおかしくありません。複雑な点が多いので、しっかりと勉強しておくことが必要です。
まず含有粒子数についてですが、上と下の面においては頂点には1/6の球が、面の中心には1/2の球があります。上下の面については簡単に求められますが、真ん中の面の含有粒子数は少し複雑なので、断面を切り取ってみましょう。
結晶格子の図では中心の3つの球しか描かれていませんでしたが、実は真ん中の面は上の図のようになっています。この図を見ると、六角形の中にはちょうど3個分の円が含まれていることがわかりますね。
したがって、真ん中の段に含まれる球は3個になります。
以上より、六方最密構造の含有粒子数は以下のようになります。
続いて、配位数について考えてみましょう。下の図の赤い粒子に注目すると、この粒子に接しているのはピンク色の粒子になります。図には現れていませんが、下側にも上側と同じように接している球が3つあります。
したがって、六方最密構造の配位数は12になります。
では次に、球の半径と結晶格子の高さの関係を求めましょう。これまでは立方体でしたが、今回は六角中なので計算するには工夫が必要です。
まずは、下の図の赤い4つの球に注目し、取り出します。これらはたがいに接しており、立体では右図のようになっています。
したがって、これら4つの球の中心を結ぶと正四面体ができます。六方最密構造の高さはちょうどこの四面体の高さの2倍として計算できますね。
四面体の高さを求める方法は何通りかありますが、今回は幾何的に解いてみます。
では最後に、六方最密構造の充填率を求めましょう。
まず、六方最密構造の充填率を出すには六角柱の体積が必要になりますね。六角柱の高さは分かっていますから、底面積を求めることになります。みなさんなら、どのように求めるでしょうか。
正六角形の面積を求める機会というのは少ないので、意外と苦戦するなと感じる人もいるでしょう。
もっとも簡単に求める方法は、下のように正六角形を6つの三角形に分ける方法になります。

以上のことから、六方最密構造には粒子が12個含まれていたので、充填率は次のように計算できます。
ここで、この0.74という数字に見覚えはありませんか。
そうです。面心立方格子の充填率と同じですよね。これらが一致するというのは、実は偶然ではありません。
なぜなら、面心立方格子と六方最密構造は粒子の積み上げ方には違いがありますが、いずれも最も密になるように粒子が敷き詰められているからです。六方最密構造に関しては名前にも最密と入っていますね。
このため、よく考えてみると配位数についてもいずれも12で一致しています。つまり、最大限まで粒子を敷き詰めると12個の粒子と接することになるということですね。
この面心立方格子と六方最密構造の類似点を知っておくと、わざわざ六方最密構造で計算するのではなく、面心立方格子の計算結果を使うという裏技ができます。
ぜひ覚えて使ってみてください。
まとめ
今回は金属結晶について解説しました。
今回の内容を表にまとめておいたので、もう一度復習しておきましょう。
金属結晶の問題は頻出であり、本番もミスなく解き切りたいところです。
したがって、少し複雑な六方最密構造も含め、それぞれの数字がどのように導かれたのかをしっかりと覚えておくようにしましょう。
最後まで読んでいただき、ありがとうございました。
それではまた!













